Turning up the heat on Earth temperature modelling

Dr Ben Mather and Prof Louis Moresi from AuScope’s Simulation, Analysis and Modelling (SAM) program have recently developed a novel, speedy and data-driven way to model the temperature of Earth’s crust in southeastern Australia. Their work has since attracted a grant from the International Association of Mathematical Geosciences (IAMG) to refine the new method and investigate earth temperatures further afield in Alaska.

Ben Mather, Jo Condon

Last updated on Feb 13, 2020 4 min read

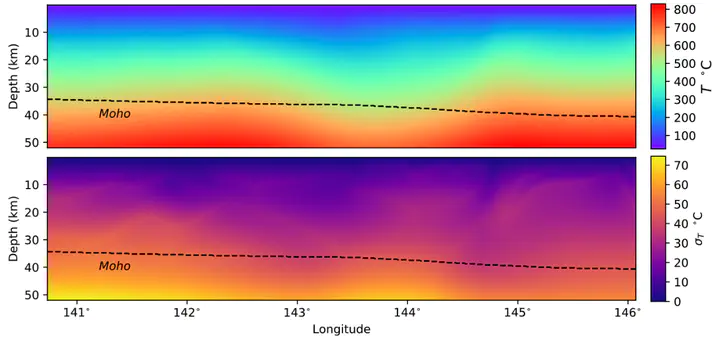For scientists, calculating the average temperature distribution in the Earth’s crust is helpful for many different geophysical and geological investigations. Understanding uncertainty in this calculation is even more helpful. This new work by Australian researchers allows scientist to do both — at a lightning pace. Pictured: the optimal temperature profile of Victoria (top) and its uncertainty (bottom). Image: Dr Ben Mather.

Article originally published by Auscope.

The SAM researchers’ method quantifies the uncertainty of Earth’s composition, making it possible to work with large numbers of unknown thermal parameters in a much shorter timeframe — hours rather than days — to quickly find an optimal temperature solution.

It pools together all data from groundwater bores and other geophysical observations to glean information on the Earth’s composition and estimating its uncertainty using Bayesian inference.

Ben from Sydney University explains:

It’s one thing to have a single “best” model, but quantifying the uncertainty around that model is even more interesting — and we were able to accomplish that.

He and Louis used the adjoint technique to detect the extent to which geological observations tell geologists about a particular model. Finding better and better solutions require running model after model with slight changes in the input parameters to find a better fit to the observations. Using some mathematics and a lot of coffee, Ben and Louis were able to speed up this process from days to mere hours.

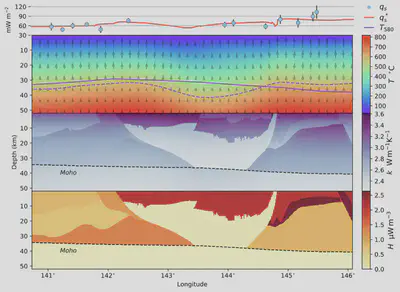
This stacked temperature section compares the misfit between simulated versus real data across a section of Victoria. The workflow requires tweaking input thermal parameters again and again until a temperature solution that best matches these data is found. Using some mathematics and a lot of coffee, Ben and Louis were able to implement their adjoint method to repeat this process only a handful of times.

Their IAMG grant will go towards building a useful open source tool for the community and apply it to a new testing ground in Alaska at unprecedented model resolution on supercomputers. The project will explore how subduction along the Aleutian trench has seeded temperature anomalies like hot springs in Alaska.

Louis from the Australian National University enthuses:

We’re excited to apply it to a new context in Alaska where very little data is currently available, the perfect ‘blank canvas’ to further refine our new method.

Ben and Louis’ work will allow scientists to better understand the Earth’s composition, and also gain insights into the geothermal and hydrocarbon potential around the world. They intend to release a Python code in late 2020 for scientists to use to achieve precise temperature predictions.

Simplified technical summary

Modelling temperature in the Earth’s crust is accomplished by populating a geological model with thermal properties, such as thermal conductivity and rates of heat production, and solving a numerical model of thermal diffusion with assigned boundary conditions.

The desired temperature solution is often the one that best matches our observations – e.g. temperature in a well – but strong assumptions are made of how thermal properties vary with depth, which result in simple first-order predictions of the temperature field.

Posing an inverse problem is a way to ascertain how much your observations tells you about a particular model. Finding better and better solutions usually require running model after model with slight changes in the input parameters to find a better fit to the observations.

For instance, a lower rate of heat production in one layer of the Earth’s crust may result in a better match to an observation of heat flow coming out of the ground. This is fine if the number of unknowns is small, but when we start to increase the quantity of unknown parameters then it takes an exponentially long time to find the model that best reproduces our observations.

In our recent paper with Prof Peter Rayner of the University of Melbourne accepted in Geophysical Journal International, we formulate a novel inversion method that uses the gradient to quickly find the optimal configuration of thermal properties that best match our observations.

We publish improved estimates of the thermal state of the crust in Victoria using heat flow measurements and Curie depth in a joint inversion using 3D geological models, and numerical models of thermal diffusion. The outcome of this work is an estimation of basal heat flux, thermal properties, and the rate of heat production for various domains in the model together with uncertainty information.